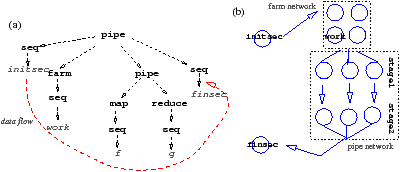
| Figure 1.1: Structure of an example CamlP3l application: (a) the skeleton nesting, (b) processes participating to the implementation: pardo, stage1 and stage2. |
CamlP3l 1.0: User ManualRoberto Di Cosmo, Zheng Li1 Marco Danelutto, Susanna Pelagatti2 Xavier Leroy, Pierre Weis, François Clément3 |
Abstract: Writing parallel programs is not easy, and debugging them is usually a nightmare. To cope with these difficulties, a structured approach to parallel programs using skeletons and template based compiler techniques has been developed over the past years by several researchers, including the P3l group in Pisa.This approach is based on the use of a set of predefined patterns for parallel computation which are really just functionals implemented via templates exploiting the underlying parallelism, so it is natural to ask whether marrying a real functional language like OCaml with the P3l skeletons can be the basis of a powerful parallel programming environment.
The CamlP3l prototype described in this document shows that this is the case. The prototype, written entirely in OCaml using a limited form of closure passing, allows a very simple and clean programming style, shows real speed-up over a network of workstations and as an added fundamental bonus allows logical debugging of a user parallel program in a sequential framework without changing the user code.
In a skeleton based parallel programming model [6, 11, 9] a set of skeletons, i.e. of second order functionals modeling common parallelism exploitation patterns are provided to the user/programmer. The programmer uses skeletons to give parallel structure to an application and uses a plain sequential language to express the sequential portions of the parallel application. He/she has no other way to express parallel activities but skeletons: no explicit process creation, scheduling, termination, no communication primitives, no shared memory, no notion of being executing a program onto a parallel architecture at all.
CamlP3l is a programming environment that allows to write parallel programs in OCaml1 according to a skeleton model derived by the one of P3l2, provides seamless integration of parallel programming and functional programming and advanced features like sequential logical debugging (i.e. functional debugging of a parallel program via execution of the architecture at all parallel code onto a sequential machine) of parallel programs and strong typing, useful both in teaching parallel programming and in building of full-scale applications3.
In this chapter, we will first discuss the goals of our system design, then recall the basic notions of the skeleton model for structured parallel programming and describe the skeleton model provided by CamlP3l, providing an informal sequential (functional) and parallel semantics. It will be then time to describe how an CamlP3l program can be compiled and run on your system (Chapter 2). Then, we discuss more CamlP3l examples (Chapter 3) and detail CamlP3l implementation (Chapter 4) describing how we achieved our goals using to our advantage the flexibility of the OCaml system.
We started the developmentof the CamlP3l in 1998. At that time, the main goal of the project was to test the possibility to integrate parallel programming in a functional language using the skeleton model: after all, as we will see later, skeletons are just functions, so a functional language should provide the natural setting for them. We also wanted to preserve the elegance and flexibility of the functional model, and the strong type system that comes with OCaml. These goals were acheved in the first version of CamlP3l.
But during the implementation of the system, it turned out that we
could get more than that: in our implementation, the sequential
semantics that is traditionally used to describe the functional
behaviour of the skeletons could actually be used to provide an
elementary library allowing to execute the user code in a sequential
mode, without modifying the user code. This is a
major advantage of the approach: in our system, the user can easily
debug the logic of his program running it with the sequential
semantics on a sequential machine using all the traditional techniques
(including tracing and step by step execution which are of no
practical use on parallel systems), and when the program is logically
correct he/she is guaranteed (assuming the runtime we provide is correct)
to obtain a correct parallel execution. Although a similar approach
has been taken in other skeleton based programming models, by
using the OCaml programming environment this result happens to be
particularly easy to achieve. This is definitely not the case of
programs written using a sequential language and directly calling
communication libraries/primitives such as the Unix socket interface
or the MPI or PVM libraries, as the logic of the program is
inextricably intermingled with low level information on
data exchange and process handling.
Following this same idea (no changes to the user code, only different
semantics for the very same skeletons), we also provided a “graphical
semantics” that produces a picture of the process network used during
the parallel execution of the user program.
Finally, we wanted a simple way to generate (from the user source code)
the various executables to be run on the different nodes of a parallel
machine: here the high level of abstraction provided by functional
programming, coupled with the ability to send closures over a channel
among copies of the same program provided the key to an elementary and
robust runtime system that consists of a
very limited number of lines of code.
But let’s first of all introduce the skeleton model of CamlP3l
1.0.
A skeleton parallel programming model supports so-called ‘structured parallel programming’ [6, 11, 9]. Using such a model, the parallel structure/behaviour of any application has to be expressed by using skeletons picked up out of a collection of predefined ones, possibly in a nested way. Each skeleton models a typical pattern of parallel computation (or form of parallelism) and it is parametric in the computation performed in parallel. As an example, pipeline and farm have been often included in skeleton collections. A pipeline just models the execution of a number of computations (stages) in cascade over a stream of input data items. Therefore, the pipeline skeleton models all those computations where a function fn(fn−1(… (f2(f1(x))) …)) has to be computed (the fi being the functions computed in cascade). A farm models the execution of a given function in parallel over a stream of input data items. Therefore, farms model all those computations where a function f(x) has to be computed independently over n input data items in parallel.
In a skeleton model, a programmer must select the proper skeletons to program his/her application leaving all the implementation/optimization to the compiler/support. This means, for instance, that the programmer has no responsibility in deriving code for creating parallel processes, mapping and scheduling processes on target hardware, establishing communication frameworks (channels, shared memory locations, etc) or performing actual interprocess communications. All these activities, needed in order to implement the skeleton application code onto the target hardware are completely in charge to the compile/run time support of the skeleton programming environment. In some cases, the support also computes some parameters such as the parallelism degree or the communication grain needed to optimize the execution of the skeleton program onto the target hardware [19, 2, 20].
In the years, the skeleton model supplied by CamlP3l has evolved. Current CamlP3l version (1.0) supplies three kinds of skeletons:
mapvector (cf. 1.3.6) and
reducevector (cf. 1.3.7).
Such skeletons are not as powerful as the
map and reduce skeletons of P3l. Instead, they closely resemble
the map (*) and reduce (/) functionals of the Bird-Meertens formalism
discussed in [3] and the map and fold skeletons in SCL
[13]. The mapvector skeleton models the parallel application of
a generic function f to all the items of a vector data structure,
whereas the reducevector skeleton models a parallel computation folding all
the elements of a vector with a commutative and associative binary
operator ⊕).
As an example, consider an application whose initial and final phase cannot be parallelized, while the behavior in the central part is clearly divided in two consecutive phases (stages) working on a stream of data. This can be modeled by the combination of CamlP3l skeletons in Fig. 1.1.

Figure 1.1: Structure of an example CamlP3l application: (a) the skeleton nesting, (b) processes participating to the implementation: pardo, stage1 and stage2.
All the structure is encapsulated in a pardo skeleton. initsec and finsec are two sequential OCaml functions describing the initial and final parts of application. The central part describes a parallel computation structured as a pipeline built out of two stages. If both stages are implemented via a sequential function (seq) data will flow as shown in Fig. 1.1.(a). In particular, the implementation spawns three processes: a ‘pardo’ process (executing the sequential parts) and a network of two processes implementing the pipeline (Fig. 1.1.(b)).
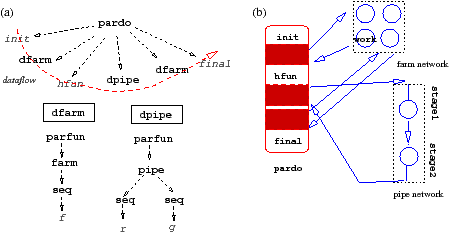
Figure 1.2: Further parallelizing the example CamlP3l application: (a) the skeleton nesting, (b) the processes participating to the implementation.
Now, suppose the programmer recognizes that
the initsec is computationally intensive and can be decomposed in a
sequential part (initsec) and a parallel part which applies a
function work
independently on
each element on a stream of input data.
In this case, we can use a farm skeleton to have a pool of replicas of
work. Moreover, suppose the function stage1 boils down
to applying a function f to all the elements of a vector and function
stage2 “sums” up all the elements of the resulting vector by using an
associative and commutative operator g.
In this case, the programmer can refine the skeleton structure by using the
combination in Fig. 1.2.
Here, the four replicas of work act on different independent
elements in the input stream, producing four stream of results (vectors) which
are merged
before entering the pipeline. Each stage is in turn implemented in parallel
using four processes. In the first stage, each input vector is partitioned
into four blocks. Each process takes care of applying f on one of
the four blocks. Then in the second stage, each process sums up the elements
in a block of the
vector and then all the partial results are added before providing the final
result back to the pardo (and to the finsec function).
The first “application outline” (Fig. 1.1) corresponds to the following (incomplete) CamlP3l code:
let initsec _ = ...;; (* generates stream *)
let finsec x = ...;; (* consumes stream *)
let stage1 _ x = ... ;;
let stage2 _ x = ... ;;
(* defines pipe network *)
let pipe = parfun (fun () -> seq(stage1) ||| seq(stage2)) ;;
pardo (fun () ->
let y = pipe (initsec ()) in
finsec y
);;
notice the use of seq skeleton to encapsulate ordinary OCaml functions and the use of parfun to define the pipe network. Here is the sketch of CamlP3l code for the second application outline (Fig. 1.2):
let degree = ref 4; (* parallel degree *)
let work _ x = ..;; (* to be farmed out *)
let f _ x = ...;; (* to be mapped *)
let g _ (x,y) = ...;; (* to be reduced *)
let pstage1 = mapvector(seq(f),!degree);;
let pstage2 = reducevector(seq(g),!degree);;
let pipe = parfun (fun () -> pstage1 ||| pstage2);;
let afarm = parfun (fun () -> farm (seq(farm_worker),!degree));;
pardo
(fun () ->
let y = pipe (afarm (initsec ())) in
finsec y
);;
here !degree refers to the number of
parallel processes to be used in the skeleton implementation of mapvector,
reducevector and farm. This value can vary in each execution of the
application without recompiling (eg., using a configuration file).
Details on how to write and run proper CamlP3l programs are
given later in Chapter 2.
In the current release, the user is supposed to explicitly give the number of
processors to be used in each farm, mapvector and reduce skeleton. In other
words the choice of the parallelism degree actually exploited in such
skeletons is up to the
programmer. It is foreseeable in a future release to ask the system to
guess optimal values depending on available resources (following the
approach of P3l [2, 19]), as it is
discussed in more detail below.
Applications with a parallel structure given by skeletons (such as the ones outlined above) can be implemented by using implementation templates [6, 19]. An implementation template is a known, parametric way of exploiting the kind of parallelism modeled by a skeleton onto a particular target architecture. As an example, a template corresponding to the mapvector skeleton will take some input vector data, it will split the data into chunks holding one or more data items of the vector, schedule them to a set of “worker” processes computing the map function f and finally collect the results and rebuild the output vector data structure. All these operations will be performed by some processes, using either communications or shared memory locations for data communication. Such a template must, as its primary goal, implement in an efficient way the mapvector skeleton and therefore:
In CamlP3l 1.0, the parallelism degree of each skeleton is chosen by the programmer. In following releases, we will explore the possibility of using analytic performance models associated with the implementation template process networks to derive the parallelism degree automatically[21]. An analytic performance model is a set of functions computing different measures of the performance achieved by a template on the basis of a small set of machine dependent and user code parameters. Examples of machine dependent parameters are the cost of communication startup and the per-byte transmission cost. Examples of user code parameters are the mean and variance of execution time for user-defined sequential parts of the program and the size of data flowing between skeletons. The models describe the template behavior as a function of the resources used (e.g. the physical number of executors in a farm) and can be used by the skeleton support to predict such behavior and to tune resource allocation. A more detailed description of the whole automatic optimization process executed by a compiler using performance models for skeleton tuning is given in [19, 20, 21].
A parallel computation in CamlP3l is defined by three components:
parfun (SF, skeleton functions in Figure 1.3)
and
pardo application.
Each time a parfun(h) functon definition is
evaluated, a corresponding
network of processes is created according to the skeleton composition in
h. Each network transforms a stream of independent input data …
x1, x0 in a
stream of output data … h(x1), h(x0) according to
h.
When a pardo is evaluated, applications of common functions boil down to
normal sequential evaluation, while applications of skeletal functions
feed arguments data to the corresponding skeletal process network and are
evaluated in parallel.
In practice, each pardo defines a network built out of all
the processes in skeletal networks (parfun defined functions) plus a
root process orchestrating
all the computation. Both the root node and the generic nodes run in SPMD
model. Initially, the root specializes all the generic nodes sending
information on the actual process to be executed (eg., a farm dispatcher, a
farm worker, a mapvector worker etc).
Then, the root process starts executing the pardo. If code is sequential, it
is executed locally on the root node. Otherwise,
if the evaluation of a parfun function is encountered,
the root activates evaluation passing the relevant parameters to the
correponding network. The same network can be activated many times,
each time an evaluation of the corresponding parfun function is
encountered.
Notice that the execution model assumes an unlimited number of homogenous processors.
In practical situations, processors will be less than processes and have
heterogeneus capacity. The CamlP3l upport, possibly with some help from the programmer
(using colors, see Sec. 1.4),
is in charge of implementing this in a transparent way.
Even if CamlP3l skeletons are close to original P3l ones, the parallel evaluation model is completely different. Thus, for these familiar with P3l, it is interesting to highlight the main differences between two models and to give a brief account on the reasons that have lead to such a design change.
In the original P3l system (and, actually in initial versions of CamlP3l[10]), a program is clearly stratified into two
levels: there is a skeleton cap, that can be composed of an
arbitrary number of skeleton combinators, but as soon as one goes
outside this cap, passing into the sequential code through the
seq combinator, there is no way for the sequential code to
call a skeleton. To say it briefly, the entry point of a P3l
program must be a skeleton expression, and no skeleton
expression is allowed anywhere else in the sequential code. Using current CamlP3l
terminology, P3l restricts the pardo to contain one single call to a network
defind with parfun, and without calls to sequential functions.
This restriction is quite reasonable when
the goal is to build a single stream processing network
described by the skeleton cap. However, it has several drawbacks in the
general case:
To overcome all these difficulties and limitations, the
1.0 version of CamlP3l introduces the new
parfun skeleton (not present in P3l), the very dual of the seq
skeleton. In simple words, one can wrap a full skeleton expression
inside a parfun, and obtain a regular OCaml stream processing
function, usable with no limitations in any sequential piece of code:
a parfun encapsulated skeleton behaves exactly as a normal
function that receives a stream as input, and returns a stream as
output. However, in the parallel semantics, the parfun
combinator gets a parallel interpretation, so that the encapsulated
function is actually implemented as a parallel network (the network to
which the parfun combinator provides an interface).
Since many parfun expressions may occur in an CamlP3l
program, there may be several disjoint parallel processing networks at
runtime. This implies that, to contrast with P3l, the
CamlP3l model of computation requiers a main sequential
program (the pardo): this main program is responsible for information interchange
with the various parfun encapsulated networks.
It is now time to discuss a simple but complete CamlP3l program. The program in Figure 1.4 uses a farm to compute a very simple function over a stream of floats.
(* computes x square *) let farm_worker _ = fun x -> x *. x;; (* prints a result *) let print_result x = print_float x; print_newline();; let compute = parfun (fun () -> (farm (seq(farm_worker),4)));; pardo(fun () -> let is = P3lstream.of_list [1.0;2.0;3.0;4.0;5.0;6.0;7.0;8.0] in let s' = compute is in P3lstream.iter print_result s'; );;
First we have two standard OCaml functions: farm_worker which
simply computes the square of a float argument and print_result which
dumps results on the stardard output. Notice that
farm_worker takes two parameters instead of one as it would seem
reasonable. The extra parameter (_) is required by the seq
skeleton type and is used in general to provide local initialization data (for
instance, an initialization matrix, some initial seed or the
like). In this simple case, initialization data are not needed and the
parameter is just ignored by farm_worker. This optional initialization
is provided for all CamlP3l skeletons (see Section 1.3.1).
Function compute uses parfun
to define a parallel network built by a single farm, in particular:
seq(farm_worker)
turns the sequential farm_worker function into a ‘stream processor’
applying it to a stream of input values. Then, an instance of the farm skeleton is defined with
farm (seq(farm_worker),4)
which spawns four workers. Finally,
parfun (fun () -> (farm (seq(farm_worker),4)));;
encapsulates the skeleton network into a standard OCaml function.
The last pardo defines how sequential functions and parallel modules
are interconnected. In this case, we have a single parallel module
(compute) and two sequential parts. The first sequential part builds up the data stream
(using the standard CamlP3l library function
P3lstream.of_list [1.0;2.0;3.0;4.0;5.0;6.0;7.0;8.0]
which turns lists in streams) and the second part
applies print_results to all the elements in the stream (using standard
stream iterator
P3lstream.iter). The global network is shown in
Figure 1.5, where arrows point out the data flow among processes.
Here we describe the syntax, the informal semantics, and the types assigned to each skeleton combinator.
Each skeleton is a stream processor, transforming an input stream into an output stream and is equipped with three semantics:
First of all, let’s explain why the actual OCaml types of our
skeleton combinators are a bit more complex than those used by other skeleton
systems (eg., [13]).
In effect, our types seem somewhat polluted by spurious
additional unit types, compared to the types one would expect.
For istance, consider the seq combinator. As informally discussed above, seq
encapsulates any OCaml function f into a sequential process which
applies f to all the inputs received in the input stream. This means that,
writing
seq f, any OCaml function with type f : 'a -> 'b
is wrapped into a sequential process (this is reminiscent to
the lift combinator used in many stream processing libraries of
functional programming languages).
Hence, a strightforward type for seq would be
('a -> 'b) -> 'a stream -> 'b stream.
However, in CamlP3l, seq is declared as
seq : (unit -> 'a -> 'b) -> unit -> 'a stream -> 'b stream
meaning that the lifted function argument f gets an
extra unit argument. In effect, in real-world application, the
user functions may need to hold a sizeable amount of local data (e.g. some
huge matrices that have to be initialised in a numerical
application), and we decided to have a type general enough to allow
the user to
finely describe where and when those data have to be initialized and/or
copied.
Reminiscent to partial evaluation and λ-lifting, we reuse the classical techniques of functional programming to initialize or allocate data globally and/or locally to a function closure. This is just a bit complicated here, due to the higher-order nature of the skeleton algebra, that in turn reflects the inherent complexity of parallel computing:
farm, a mapvector or a reducevector may launch; this was
already available in the previous versions of CamlP3l, since we
could write
let f = let localdata = do_huge_initialisation_step () in fun x -> compute (localdata, x);; … farm (seq f, 10)
farm or a mapvector skeleton; this was just impossible
in the previous versions of CamlP3l; with unit types, it is
now easy to achieve:
let f () = let localdata = do_huge_initialisation_step () in fun x -> compute (localdata, x);; … farm (seq f, 10)when the
farm skeleton creates 10 copies of seq f,
each copy is created by passing () to the seq combinator,
which in turn passes () to f, producing the allocation of a
different copy of localdata for each instance4.Note also that the old behaviour, namely CamlP3l version 1.0, where a unique initialization was shared by all copies, is still easy (and can be freely combined to further local initializations if needed):
let f = let localdata = do_huge_initialisation_step () in fun () -> fun x -> compute (localdata, x);; … farm (seq f, 10)
To sum up, the extra unit parameters give the programmer the
hability to decide whether local initialisation data in his functions
are shared among all copies or not. In other words, we can regard the
skeleton combinators in the current version of CamlP3l as
“delayed skeletons”, or “skeleton factories”, that produce an
instance of a skeleton every time they are passed an () argument.
In the following sections we detail the types and semantics of all the skeletons and provide some usage examples.
The seq skeleton encapsulates an OCaml function f into a stream process which applies f to all the inputs received on the input stream and sends off the reselts on the output stream. Any OCaml function with type
f: unit -> 'a -> 'b
can be encapsulated in the seq skeletons as follows:
seq f
The central point is that the function must be unary, i.e. functions working on more that one argument must collect them in a single tuple before being used in a seq. For instance, the fragment
let g _ (x,y) = x *. y;; let redmul = parfun (fun () -> reducevector(seq(g),6));;
shows how to encapsulate a float binary operator (*.) to use it within a reducevector with 6 working processes.
The farm skeleton computes in parallel a function f over
different data items appearing in its input stream.
From a functional viewpoint, given
a stream of data items x1, …, xn, and a function f, the
expression farm (f, k) computes f(x1), …, f(xn).
Parallelism is gained by having k independent processes that
compute f on different items of the input stream.
If f has type (unit -> ’b stream -> ’c stream), and
k has type int, then farm (f, k) has type
unit -> ’b stream -> ’c stream.
In terms of (parallel) processes, a sequence of data appearing onto
the input stream of a farm is submitted to a set of worker processes.
Each worker applies the same function (f, which can be in turn difined
using parallel skeletons) to the data items
received and delivers the result onto the output stream. The resulting
process network looks like the following:

where the emitter process takes care of task-to-worker scheduling (possibly taking into account some load balancing strategy).
The farm function takes two parameters:
Figure 1.6 shows an CamlP3l program which chooses randomly a number from a list and writes it to the file magic_number. Notice the local initialization of the random number generator (which takes a different seed in each worker) and the local open of the file to be written. In Figure 1.7 you can see how the worker code can be simply transformed to have all the workers share the same filed descripto if needed (global initialization).
let write_int = function () -> let fd = Unix.openfile "magic_number" [Unix.O_WRONLY; Unix.O_CREAT; Unix.O_TRUNC] 0o644 in let () = Random.self_init () in ( function x -> let time_to_wait = 1 + (Random.int 3) in Unix.sleep(time_to_wait); let sx = string_of_int x in ignore(Unix.write fd sx 0 (String.length sx));; let parwrite = parfun(fun () -> farm(seq(write_int), 5));; pardo( fun () -> let the_stream = P3lstream.of_list [0;1;2;3;4] in parwrite the_stream );;
let write_int = let fd = Unix.openfile "magic_number" [Unix.O_WRONLY; Unix.O_CREAT; Unix.O_TRUNC] 0o644 in ( function () -> let () = Random.self_init () in function x -> let time_to_wait = 1 + (Random.int 3) in Unix.sleep(time_to_wait); let sx = string_of_int x in ignore(Unix.write fd sx 0 (String.length sx));;
The pipeline skeleton is denoted by the infix
operator |||; it performs in parallel the computations relative
to different stages of a function composition over different data
items of the input stream.
Functionally, f1 ||| f2 … |||
fn computes fn (… f2 (f1 (xi))…) over all the data
items xi in the input stream. Parallelism is now gained
by having n independent parallel processes. Each process computes
a function fi over the data items produced by the process computing
fi−1 and delivers its results to the process computing
fi+1.
If f1 has type (unit -> ’a stream -> ’b stream),
and f2 has type (unit -> ’b stream -> ’c stream),
then f1 ||| f2 has type unit -> ’a stream -> ’c stream.
In terms of (parallel) processes, a sequence of data appearing onto the input stream of a pipe is submitted to the first pipeline stage. This stage computes the function f1 onto every data item appearing onto the input stream. Each output data item computed by the stage is submitted to the second stage, computing the function f2 and so on and so on until the output of the n−1 stage is submitted to the last stage. Eventually, the last stage delivers its own output onto the pipeline output channel. The resulting process network looks like the following:

For instance, a pipeline made out of three stages, the first one squaring integers, the second one multiplying integers by 2 and the third one incrementing integers can be written as follows:
let square _ x = x * x;; let double _ x = 2 * x;; let inc _ x = x + 1;; let apipe = parfun (fun () -> seq(square) ||| seq(double) ||| seq(inc));;
A pipeline models (parallel) function composition, thus input and output types
of stages should match. This means that
if stage (i−1) has type
unit -> 'c -> 'a
stage (i+1) has type
unit -> 'b -> 'd
stage i-th must have type
unit -> 'a -> 'b.
The loop skeleton named loop; it computes a function f over all the elements of its input stream until a boolean condition g is verified. A loop has type
('a -> bool) * (unit -> 'a stream -> 'a stream)
provided that f has type unit -> 'a stream -> 'a stream
and g has type 'a -> bool.
Function f is computed before testing termination, thus it is applied at
least one time to each input stream element.
In terms of (parallel) processes, a sequence of data appearing onto
the input stream of a loop is submitted to a loop in stage. This
stage just merges data coming from the input channel and from the
feedback channel and delivers them to the loop body stage. The
loop body stage computes f and delivers results to the loop end
stage. This latter stage computes g and either delivers (f x) onto the
output channel (in case (g (f x)) turns out to be true) or it
delivers the value to the loop in process along the feedback channel
((g (f x)) = false).
The resulting process network looks like the following:

For instance, the following loop increments all the integer data items in the input stream until they become divisible by 5:
let notdivbyfive x = (x mod 5 <> 0);; let inc _ x = x + 1;; let aloop = parfun (fun () -> loop(notdivbyfive,seq(inc)));;
The output of this function on the sequence
3,7,10,14
is 5,10,15,15. In particular, the call theloop 10 returns 15 as the body seq(inc) is evaluated on input data before the condition, and therefore the first time the condition is evaluated on 11 and not on 10.
The map skeleton is named mapvector; it
computes in parallel a function over all the data items of a vector,
generating the (new) vector of the results.
Therefore, for each vector X in the input data stream,
mapvector (f, n) computes the function f over all the
items of X=[x1,… , xn], using n distinct parallel processes that compute f
over distinct vector items ([f(x1),… , f(xn)]).
If f has type (unit -> ’a stream -> ’b stream), and n
has type int, then mapvector (f, n) has type
unit -> ’a array stream -> ’b array stream.
In terms of (parallel) processes, a vector appearing onto the input stream of a mapvector is split n elements and each element is computed by one of the n workers. Workers apply f to the elements they receive. A collector process is in charge of gluing together all the results in a single result vector.

Different strategies can be used to distribute a vector [|x1;...;xm|]
appearing in the input data stream to the workers.
As an example the emitter:
xi to the workers
({w1,...wn}). The workers in this case simply compute the
function f : ′a → ′b over all the elements appearing onto
their input stream (channel).
Summarizing, the emitter process takes care of (sub)task-to-worker scheduling (possibly implementing some kind of load balancing policy), while the collector process takes care of rebuilding the vector with the output data items and of delivering the new vector onto the output data stream. mapvector takes two arguments:
For instance, the following code works on a stream of integer vectors and squares each vector element. The skeleton has a parallelism degree of 10, that is ten parallel processes are used to compute each vector in the stream.
let square _ x = x * x;; let amap = parfun (fun () -> mapvector(seq(square),10));;
the result on a single array is as follows
# amap [|1;2;3;4;5|];; - : int array = [|1; 4; 9; 16; 25|]
The reduce skeleton is named reducevector; it folds
a function over all the data items of a vector.
Therefore, reducevector (⊕, n) computes x1 ⊕ x2
⊕ … ⊕ xn out of the vector x1, …, xn, for each
vector in the input data stream. The computation
is performed using n different parallel processes that compute f.
If ⊕ has type (unit -> ’a * ’a stream -> ’a stream),
and n has type int, then
reducevector(⊕, n) has type unit -> ’a array stream -> ’a
stream.
In terms of (parallel) processes, a vector appearing onto the input stream of a reducevector is processed by a logical tree of processes. Each process is able to compute the binary operator g. The resulting process network looks like the following tree:

In this case, the emitter process is the one delivering either couples
of input vector data items or couples of sub-vectors of the input
vector to the processes belonging to the tree base. In the former
case, log(n) levels of processes are needed in the tree, in the
latter one, any number of process levels can be used, and the number
of sub-vectors to be produced by the emitter can be devised
consequently.
The reducevector function takes two parameters as usual:
For instance, the following skeleton instance accepts in input a stream of vectors and, for each vector, computes the sum of all elements using the arithmetic + operator.
let areduce = parfun (fun () -> reducevector(seq(fun _ (x,y) -> x + y),10));;
the result on a single array is as follows
# areduce [|1;2;3;4|];; - : int = 10
One would expect parfun to have type (unit -> ’a stream -> ’b stream) -> ’a stream -> ’b stream: given a skeleton expression with type (unit -> ’a stream -> ’b stream), parfun returns a stream processing function of type ’a stream -> ’b stream.
parfun’s actual type introduces an extra level of functionality: the argument is no more a skeleton expression but a functional that returns a skeleton:
val parfun : (unit -> unit -> ’a stream -> ’b stream) -> ’a stream -> ’b stream
This is necessary to guarantee that the skeleton wrapped in a
parfun expression will only be launched and instanciated by
the main program (pardo), not by any of the multiple running copies of the
SPMD binary, even though thoses copies may evaluate the
parfun skeletons; the main program will actually create the
needed skeletons by applying its functional argument, while the
generic copies will just throw the functional away, carefully avoiding
to instanciate the skeletons.
Finally, the pardo combinator defines the scope of the expressions that may use the parfun encapsulated expressions.
val pardo : (unit -> ’a) -> ’a
pardo takes a thunk as argument, and gives back the result of its evaluation. As for the parfun combinator, this extra delay is necessary to ensure that the initialization of the code will take place exclusively in the main program and not in the generic SPMD copies that participate to the parallel computation.
In order to have the parfun and pardo work correctly together
the following scoping rule has to be sollowed:
Due to the scoping rule in the pardo, the general structure of an CamlP3l program looks like the following:
(* (1) Functions defined using parfun *) let f = parfun(skeleton expression) let g = parfun(skeleton expression) (* (2) code referencing these functions under abstractions *) let h x = … (f …) … (g …) … …
(* NO evaluation of code containing a parfun is allowed outside pardo *) …
(* (3) The pardo occurrence where parfun encapsulated functions can be called. *) pardo (fun () -> (* NO parfun combinators allowed here *) (* code evaluating parfun defined functions *) … let a = f … let b = h … … ) (* finalization of sequential code here *)
At run time, in the sequential model, each generic copy just waits for instructions from the main node; the main node first evaluates the arguments of the parfun combinators to build a representation of the needed skeletons; then, upon encountering the pardo combinator, the main node initializes all the parallel computation networks, specialising the generic copies (as described in details in [10]), connects these networks to the sequential interfaces defined in the parfun’s, and then runs the sequential code in its scope by applying its function parameter to ():unit. The whole picture is illustrated in Figure 1.3. The skeleton networks are initiated only once but could be invoked many times during the execution of pardo.
In the CamlP3l system, the combinators expressions govern the shape of the process network and the execution model assumes a ‘virtual’ processor, for each process. The mapping of virtual to physical processors is delegated to the CamlP3l system. The mapping is currently not optimized in the system. However, programs and machines can be annotated by the programmer using colors, which can pilote the virtual-to-physical mapping process.
The idea is to have the programmer to rank the relative ‘weight’ of skeleton instances and the machine power in a range of integer values (the colors). Then, weights are used to generate a mapping in which load is evenly balanced on the partecipating machine according to their relative power.
Pushing the difficult part of the generaion of weights to the programmer’s knowledge and ability, this simple and practical idea gives surprisingly good results in practice.
Let’s consider as an example, the skeletal expression we discussed in the example (Sec 1.2.3):
| farm (seq (fun x → x * x), 16) |
that corresponds to a network of one emitter node, one collector node, and 16 worker nodes which compute the square function. There are numerous ways of mapping a set of virtual nodes to a set of physical nodes.
If no information is provided, the support uses a simple round robin, which maps virtual to physical nodes in a cyclic way: first all phisical processors get one process then we start again from the beginning until virtual processors are all allocated. Unfortunately, such a solution doesn’t take into account the load balancing constraints: all the physical (resp. virtual) nodes are considered equivalent in computing power and are used evenly.
If the programmer knows more about machines and processes he/she can tell
the system using colors.
A color is an optional integer parameter that is added to
CamlP3l expressions in the source program and to the execution
command line of the compiled program. We use the regular OCaml’s
optional parameters syntax, with keyword col, to specify the
colors of a network of virtual nodes. For example, writing
farm ~col:k (f, n)
means that all virtual nodes inside this farm structure
should be mapped to some physical nodes with a capability ranking
k. The scope of a color specification covers all the inner nodes of
the structure it qualifies: unless explicitely specified, the color of
an inside expression is simply inherited from the outer layer (the
outermost layer has a default color value of 0 which means no special
request).
For combinators farm, mapvector and reducevector, in addition to the color of the combinator itself, their is an additional optional color parameter colv. A colv[ ] specification is a color list (i.e. an int list) that specifies the colors of the parallel worker structures that are arguments of the combinator. As an example, the CamlP3l expression
map ~col:2 ~colv:[ 3; 4; 5; 6 ] (seq f, 4)
is a mapvector skeleton expression, with emitter and
collector nodes of rank 2, and four worker nodes (four copies of
seq f) whith respective ranks 3, 4, 5, and 6.
To carefully map virtual nodes to physical nodes, we also need a way to define the colors of physical nodes. This information is specified on the command line when launching the program (see Section 2). One can write:
prog.par -p3lroot ip1:port1#color1 ip2:port2#color2 ... \
ip_i:port_i#color_i ...
where ip_i:port_i#color_i indicates the ip address (or name), the port, and the color of the physical node i participating to the computation. The port and color here are both optional. With no specified port, a default p3lport is used; with no color specification, the default color 0 is assumed.
If the colors of all the virtual processors and all the physical processors have a one-to-one correspondance, the mapping is easy. But such a perfect mapping does not exist in general: first of all, there is not always equality between the amount of physical processors we have and the amount of virtual processors we need; second, in some very complex CamlP3l expressions, it is complex and boring for the programmer to calculate manually how many virtual nodes are needed for each color class.
So, we decided to use a simple but flexible mapping algorithm, based on the idea that what a color means is not the exact capability required but the lowest capability acceptable. For example, a virtual node with color value 5 means a physical node of color 5 is needed, but if there is no physical node with value 5, and there exists a physical node of color 6 free and available, why don’t we take it instead? In practice, we sort the virtual nodes in decreasing order of their color values, to reflect their priority in choosing a physical node: virtual nodes with bigger colors should have more privilege and choose their physical node before the nodes with smaller colors. Then, for each virtual node, we lists all the physical nodes with a color greater than or equal to the virtual node color. Among all those qualified ones, the algorithm finally associates the virtual node with the qualified node which has the smallest work load (the one that has the least number of virtual nodes that have been assigned to it).
This algorithm provides a mapping process with some degree of automatization and some degree of manual tuning, but one has to keep in mind that the color designs a computational class, qualitatively, and is not an exact quantitative estimation of the computational power of the machine, as the current version of CamlP3l does not provide yet the necessary infrastructure to perform an optimal mapping based on precise quantitative estimations of the cost of each sequential function and the capabilities of the physical nodes, so that we cannot guarantee our color-based mapping algorithm to be highly accurate or highly effective.
Still, the “color” approach is accurate and simple enough to be quite significant to the programmer: according to the experiments we have conducted, it indeed achieved some satisfactory results in our test bed case (see [5]).
Figure 1.8 summarizes the types of the combinators, exactly as they are currently available to the programmer in the 1.0 version of CamlP3l, including the optional color parameters.
type color = int val seq : ?col:color -> (unit -> ’a -> ’b) -> unit -> ’a stream -> ’b stream val ( ||| ) : (unit -> ’a stream -> ’b stream) -> (unit -> ’b stream -> ’c stream) -> unit -> ’a stream -> ’c stream val loop : ?col:color -> (’a -> bool) * (unit -> ’a stream -> ’a stream) -> unit -> ’a stream -> ’a stream val farm : ?col:color -> ?colv:color list -> (unit -> ’b stream -> ’c stream) * int -> unit -> ’b stream -> ’c stream val mapvector : ?col: color -> ?colv:color list -> (unit -> ’b stream -> ’c stream) * int -> unit -> ’b array stream -> ’c array stream val reducevector : ?col:color -> ?colv:color list -> (unit -> (’b * ’b) stream -> ’b stream) * int -> unit -> ’b array stream -> ’b stream val parfun : (unit -> unit -> ’a stream -> ’b stream) -> ’a stream -> ’b stream val pardo : (unit -> ’a) -> ’a
We give here a practical tutorial on how to use the system, without entering into the implementation details of the current version of CamlP3l.
As mentioned above, once you have written an CamlP3l program, you have several choices for its execution, since you can without touching your source:
Presumably, you would run the parallel version once the program has satisfactorily passed the sequential debugging phase.
In the following sections, our running example is the computation of a Mandelbrot fractal set. We will describe the implementation program, compile it and run it in the three ways described above.
The Mandelbrot example program performs the calculation of the Mandelbrot set at a given resolution in a given area of the graphic display. This is the actual program provided in the Examples directory of the distribution.
The computing engine of the program is the function pixel_row which computes the color of a row of pixels from the convergence of a sequence of complex numbers zn defined by the initial term z0 and the formula zn + 1 = zn2 + z0. More precisely, given a point p in the complex plane, we associate to p the sequence zn when starting with z0 = p. Now, we compute the integer m such that zm is the first term of the sequence satisfying the following condition: either the sum of the real and imaginary parts of zn exceeds a given threshold, or the number of iterations exceeds some fixed maximum resolution limit. Integer m defines the color of p.
p). This correspond to the following OCaml code:
open Graphics;;
let n = 300;; (* the size of the square screen windows in pixels *)
let res = 100;; (* the resolution: maximum number of iterations allowed *)
(* convert an integer in the range 0..res into a screen color *)
let color_of c res = Pervasives.truncate
(((float c)/.(float res))*.(float Graphics.white));;
(* compute the color of a pixel by iterating z_m+1=z_m^2+c *)
(* j is the k-th row, initialized so that j.(i),k are the coordinates *)
(* of the pixel (i,k) *)
let pixel_row (j,k,res,n) =
let zr = ref 0.0 in
let zi = ref 0.0 in
let cr = ref 0.0 in
let ci = ref 0.0 in
let zrs = ref 0.0 in
let zis = ref 0.0 in
let d = ref (2.0 /. ((float n) -. 1.0)) in
let colored_row = Array.create n (Graphics.black) in
for s = 0 to (n-1) do
let j1 = ref (float j.(s)) in
let k1 = ref (float k) in
begin
zr := !j1 *. !d -. 1.0;
zi := !k1 *. !d -. 1.0;
cr := !zr;
ci := !zi;
zrs := 0.0;
zis := 0.0;
for i=0 to (res-1) do
begin
if(not((!zrs +. !zis) > 4.0))
then
begin
zrs := !zr *. !zr;
zis := !zi *. !zi;
zi := 2.0 *. !zr *. !zi +. !ci;
zr := !zrs -. !zis +. !cr;
Array.set colored_row s (color_of i res);
end;
end
done
end
done;
(colored_row,k);;
In this code, the global complex interval sampled stays within (-1.0, -1.0) and (1.0, 1.0). In this 2-unit wide square, the pixel_row functions computes rows of pixels separated by the distance d. The pixel_row function takes four parameters: size, the number of pixels in a row; resolution, the resolution; k, the index of the row to be drawn; and, j, an array which will be filled with the integers representing the colors of pixels in the row. These values will be converted into real colors by the color_row function. In this program, the threshold is fixed to be 4.0. We name zr and zi the real and imaginary parts of zi; similarly, the real and imaginary parts of c are cr and ci; zrs and zis are temporary variables for the square of zr and zi; d is the distance between two rows.
The Mandelbrot computation over the whole set of points within (-1.0,-1.0) and (1.0,1.0) in the complex plane can be computed in parallel exploiting farm parallelism. The set of points is split by gen_rows into a bunch of pixel rows that build up the input stream, the computation of the Mandelbrot set on each row of complex points is independent and can be performed by the worker processes using pixel_row and the result is a stream of rows of pixel colors, each corresponding to an input pixel row.
(* draw a line on the screen using fast image functions *)
let show_a_result r =
match r with
(col,j) ->
draw_image (make_image [| col |]) 0 j;;
(* generate the tasks *)
let gen_rows =
let seed = ref 0 in
let ini = Array.create n 0 in
let iniv =
for i=0 to (n-1) do
Array.set ini i i
done; ini in
(function () ->
if(!seed < n)
then let r = (iniv,!seed,res,n) in (seed:=!seed+1;r)
else raise End_of_file)
;;
The actual farm is defined by the mandel function which uses the
parfun skeleton to transform a farm instance with 10 workers into an
OCaml sequential function. Notice that the seq
skeleton has been used to turn the pixel_row function into a stream
process, which can be used to instantiate a skeleton.
Finally the pardo skeleton takes care of opening/closing a
display window on the end-node (the one running pardo), and of
actually activating the farm invoking mandel. The function
show_a_result actually displays a pixel row on the end-node. Notice
that this
code would need to be written anyway, maybe arranged in a different way, for a
purely sequential implementation.
(* the skeleton expression to compute the image *)
let mandel = parfun (fun () -> farm(seq(pixel_row),10));;
pardo (fun () ->
print_string "opening...";print_newline();
open_graph (" "^(string_of_int n)^"x"^(string_of_int n));
(* here we do the parallel computation *)
List.iter show_a_result
(P3lstream.to_list (mandel (P3lstream.of_fun gen_rows)));
print_string "Finishing";print_newline();
for i=0 to 50000000 do let _ =i*i in () done;
print_string "Finishing";print_newline();
close_graph()
)
We assume the program being written in a file named mandel.ml. We compile the sequential version using camlp3lc as follows:
camlp3lc --sequential mandel
open Seqp3l;;
to obtain a temporary file mandel.seq.ml which is then compiled via the regular Caml compiler ocamlc with the proper modules and libraries linked. Depending on the configuration of your system, this may look like the following
ocamlc -custom unix.cma graphics.cma seqp3l.cmo
-o mandel.seq mandel.seq.ml
-cclib -lunix -cclib -lgraphics -cclib -L/usr/X11R6/lib
-cclib -lX11
We highly recommend not to use explicit call to ocamlc: use the camlp3lc compiler that is especially devoted to the compilation of CamlP3lprograms. ⋄
After the compilation, we get an executable file, mandel.seq, whose execution produces the picture shown on the left side of 2.1.

Figure 2.1: A snapshot of the execution of mandel.ml (left is sequential execution, right is parallel execution on 5 machines).
It is often useful to look at the structure of the application process network, for example when tuning the performance of the final program. In CamlP3l, this can be done by compiling the program with the special option --graphical which automatically creates a picture displaying the ‘logical’ parallel program structure.
camlp3lc --graphical mandel.ml
In the current implementation, this boils down to adding on top of mandel.ml the line
open Grafp3l;;
to obtain a temporary file mandel.gra.ml which is then compiled via ocamlc with the proper modules and libraries. Depending on the configuration of your system, this may look like the following
ocamlc -custom graphics.cma grafp3l.cmo -o mandel.gra mandel.gra.ml
-cclib -lgraphics -cclib -L/usr/X11R6/lib -cclib -lX11
Once more, we highly recommend not to use explicit calls to ocamlc: use the camlp3lc compiler that is especially devoted to the compilation of CamlP3lprograms. ⋄
After compilation, we get the executable file mandel.gra, whose execution produces the following picture.

Once we have checked the sequential version of our code, and got a picture of the structure of the parallel network, we are ready to speed up the computation by using a network of computers.
We call the compiler with the special option --parallel devoted to compilation for parallel execution:
camlp3lc --parallel mandel
open Parp3l;; open Nodecode;; open Template;;
to obtain a temporary file mandel.par.ml which is then compiled via ocamlc with the proper modules and libraries. Depending on the configuration of your system, this may look like the following
ocamlc -custom unix.cma p3lpar.cma -o mandel.par mandel.par.ml
-cclib -lunix -cclib -lgraphics -cclib -L/usr/X11R6/lib
-cclib -lX11
Once again, we highly recommend not to use explicit calls to ocamlc: use the camlp3lc compiler that is especially devoted to the compilation of CamlP3lprograms. ⋄
The compilation produces an executable file named mandel.par.
The parallel compilation of CamlP3l programs creates executables that are equipped with the following set of predefined options:
-p3lroot, to declare this invocation of the program as the root node.-dynport, to force this node to use a dynamic port number instead
of the default p3lport; in addition the option outputs it (useful if
you want to run more slave copies on the same machine).-debug, to enable debugging for this node at level n. Currently all
levels are equal.-ip, to force the usage of a specified ip address. Useful when you
are on a laptop named localhost and you want to be able to choose among
network interfaces.-strict, to specify a strict mapping between physical and virtual
processors.-version, to print version information.-help or --help Displays this list of options.The executable produced by using the --parallel option of the compiler behaves either as a generic computation node, or as the unique root configuration node, according to the set of arguments provided at launch time.
To set up and launch the parallel computation network, we need to run multiple invocations of the parallel executable:
As soon as created, the root node configures all other participating nodes and
then executes locally the pardo encapsulated sequential code.
In addition to the -p3lroot special option, the root node invocation must specify the information concerning the machines involved in the computational network (their ip address or name, their port and color).
Here is a simple script to launch the parallel network on several machines:
#!/bin/sh
# The list of machines
NODES="machine1 machine2 machine3 machine4"
# The name of executable to be launched
PAR="./mandel.par"
echo -n "Launching CamlP3l $PAR on the cluster:"
for NODE in $NODES; do #(*1*)
echo -n " $NODE"
#launching a generic computation node on each machine
ssh $NODE $PAR 1> log-$NODE 2> err-$NODE &
# a possible coloring of machines
case $NODE in #(*2*)
machine1) COLORED_NODES="$COLOREDNODES $NODE#1";;
*) COLORED_NODES="$COLOREDNODES $NODE#2";;
esac
done
echo "Starting computation with $COUNT node(s): $COLORED_NODES..."
# launch the unique root configuration node #(*3*)
$PAR -p3lroot $COLOREDNODES 1> log-root 2> err-root
echo "Finished."
This script assumes mandel.par to be accessible to all participating
machines and does the following:
mandel.par on all participating machines
(#(*1*)),
#(*2*)),
#(*3*)) providing the list of colored participating hosts.
In future versions, especially those incorporating the MPI communication layer, the startup mechanism will possibly work differently (typically, the initialization steps will be performed by the MPI layer).
A few words of warning now: even if the user program is now easy to write, compile and execute, you should not forget that the underlying machinery is quite sophisticated, and that in some situations you may not get what you expected. Two typical problems you may encounter are the following:
Streams to be feed to the parallel networks can be created and consumed using functions in P3lstream. Main functions are as follows:
Function Description Secs P3lstream.of_list transforms a list in a valid stream 3.1.1, 3.1.2, 3.5 P3lstream.iter iterates on all elements of a stream 3.1.1, 3.1.2, 3.1.3 P3lstream.of_fun allows stream generation iterating a sequential function which explicitely raises End_Of_File3.1.3 P3lstream.to_list transforms streams into lists 3.1.4
let rec generate_list_of_float n s =
if ( n <= 0 ) then []
else s :: (generate_list_of_float (n-1) (s +. 1.0))
;;
let initseq n s = P3lstream.of_list (generate_list_of_float n s);;
let finseq y =
P3lstream.iter (fun x -> print_float x; print_newline()) y;;
(* Define stage1 and stage 2, can be anything......*)
let stage1 _ x = x +. x;;
let stage2 _ x = x *. x;;
(* definizione network del pipe *)
let pipe = parfun (fun () -> seq(stage1) ||| seq(stage2));;
(* pardo activation *)
pardo
(fun () ->
let s = initseq 10 1.0 in
let y = pipe s in
finseq y
);;
let read_input_float fd =
Scanf.fscanf fd "%f" (fun n -> n);;
let rec fgenerate_list_of_float cin n=
if ( n <= 0 ) then []
else
(try
(let s = (read_input_float cin) in
Printf.printf "Ecco %f\n" s;
s:: (fgenerate_list_of_float cin (n-1)))
with
End_of_file -> [];
)
;;
(* stream generation *)
let initseq cin n =
P3lstream.of_list (fgenerate_list_of_float cin n);;
(* prints out stream *)
let finseq cout y =
P3lstream.iter (fun x -> Printf.fprintf cout "%f" x; output_string cout "\n") y;;
(* Defines stage1 and stage 2 *)
let stage1 _ x = x +. x;;
let stage2 _ x = x *. x;;
(* defining a two stage pipe network *)
let pipe = parfun (fun () -> seq(stage1) ||| seq(stage2));;
(* pardo activation *)
pardo
(fun () ->
let cin = open_in "pippo" and cout = open_out "pluto" in
let s = initseq cin 10 in
let y = pipe s in
finseq cout y
)
;;
Here, the stream is generated by repeatedly calling function
generate_input_stream via P3lstream.of_fun.
%quinto-esempioUM.ml
(* generating the input stream calling repetedly a function *)
let generate_input_stream =
let x = ref 0.0 in
(function () ->
begin
x := !x +. 1.0;
if(!x < 10.0) then !x else raise End_of_file
end);;
(* prints out an integer stream *)
let finseq y =
P3lstream.iter (fun x -> print_float x; print_newline()) y;;
(* Defines stage1 and stage 2 as identity*)
let stage1 _ x = x;;
let stage2 _ x = x;;
let pipe = parfun (fun () -> seq(stage1) ||| seq(stage2));;
(* pardo activation *)
pardo
(fun () ->
let s = P3lstream.of_fun generate_input_stream in
let y = pipe s in
finseq y
)
;;
(* generating the input stream calling repeatedly a function *)
let generate_input_stream =
let x = ref 0.0 in
(function () ->
begin
x := !x +. 1.0;
if(!x < 10.0) then !x else raise End_of_file
end);;
(* Defines stage1 and stage 2*)
let stage1 _ x = x +. 1.;;
let stage2 _ x = x +. 7.;;
let print_result x =
print_float x; print_newline();;
let pipe = parfun (fun () -> seq(stage1) ||| seq(stage2));;
(* pardo activation *)
pardo
(fun () ->
let is = P3lstream.of_fun generate_input_stream in
(* transforms a stream into a list *)
let l = P3lstream.to_list (pipe is) in
List.iter print_result (List.map (fun n -> n*. 4.) l)
)
;;
As discussed in Section2.7, global variables must not be used in an CamlP3l pragram, as their value on different processing nodes will be different and updates will have effect only on the node which executes them.
On the other hand, we can have both local and global definitions which are evaluated before or after specializing a procesing node. For instance we can share the same file descriptor between all the processing nodes partecipating to a skeleton. See examples in Section 1.3.3.
To be done
To be done
The following code defines a farm in which each worker computes the square over a stream of float. However, the function is computed by an external command which is spawned and connected via stdin / stdout to the farm worker in the seq skeleton. In the following code, care is taken to activate the external process only once. spawned is true only if the Unix process and connecting pipes descriptor are maintained in variables cin and cout. Notice that pattern matching in (* * *) is not exhaustive, because if process has been already spawned cin and cout must contain a valid descriptor.
let farm_worker _ =
let conto = ref 0 and spawned = ref false
and cin = ref None
and cout = ref None in
(fun x ->
conto := !conto + 1;
if not !spawned then
begin
let (ic,oc) = Unix.open_process "./square"
in cin := Some ic; cout := Some oc; spawned:=true
end;
let Some ic, Some oc = (!cin , !cout) in (* * *)
Printf.fprintf oc "%d\n" x; Pervasives.flush oc;
let i = Scanf.fscanf ic "%d" (fun x -> x) in
)
;;
let compute = parfun (fun () -> farm(seq(farm_worker),4));;
let print_result x = print_int x; print_newline();;
pardo(fun () ->
let is = P3lstream.of_list [1;2;3;4;5;6;7;8;9] in
let s' = compute is in P3lstream.iter print_result s';
);;
The important thing is remember to fflush data output in the external commend source otherwise we block. The following is an example of valid C definition for the square program.
#include <stdio.h>
#define TRUE 1
int main(void)
{
int i;
while (TRUE) {
/* reading from standard input */
scanf("%d",&i);
/* writing on strandard output */
printf("%d\n",i*i);
/* fflushing buffers otherwise you block the output stream */
fflush(NULL);
}
exit(0);
}
Now, let us point out the peculiar features relative to the implementation of CamlP3l. First, we will discuss the mechanism used to implement different processes onto different nodes, by exploiting a particular form of “closure communication”. Then, we will point out some details relative to the interprocess communication layer and we will motivate the choice of the Unix sockets as the CamlP3l communication layer. Finally, we will discuss some details of the templates we used to implement the skeletons provided by CamlP3l.
A sequential implementation of an CamlP3l program is quite
easy to provide: just use a library seqp3l.ml which implements each
skelton with a valid OCaml sequential function.
The type safety is a direct consequence of the
fact that we are not
using here anything from outside the safe core of Ocaml.
Similarly, providing the graphical semantics poses no real challenge.
But what about the parallel semantics? What is the right way to implement such a thing? We must guarantee the type safety and ensure that the runtime is reasonably small as to allow the verification of its properties, which will become an important point in industrial applications. Both points posed problems which we overcame during the development of the system.
First of all, to ensure that the system is manageable and safe, we immediately discarded the approach based on parsing the source file to extract the code corresponding to each node of the network: this would impose to use external tools to perform an analysis of the user code which is difficult, error prone, and whose semantics would have a very unclear status.
Instead, we choose to use an SPMD approach: all the nodes of the network will run the same program (in a sense this is the “template process interpreter code”, as we will see in while) , which will be the result of the compilation of the full user code, and a control node1 will dispatch to the rest of the nodes in the network the parameterization information needed to specialize it to the particular function it is really supposed to perform (emitter, collector, sequential node running a given function f, etc.).
In order to achieve this behavior, the control node performs the following tasks:
This very last task requires a sophisticated operation: sending a function (or a closure) over a communication channel. This is usually not possible in traditional functional programming languages, since sending an arbitrary function supposes that we are able to find on the receiving side the code corresponding to the function name received or that we can transfer executable code (a feature known as mobility today). Now, mobility is necessary to send closures between arbitrary programs (since two different programs have no reason to know each other’s function code), but not between two copies of the same program: in the latter case, it suffices to send what essentially amounts to a code pointer. Starting from version 1.06, OCaml contains a modified marshaling library, originary designed for the CamlP3l system, that performs closure sending between copies of the same program (this is checked by means of an MD5 signature of the program code). The ocaml run time system takes care of dealing with differences in endianness and word size between communicating machines, as well as flattening tree-shaped data structures.
On the other side, all the other nodes simply wait for a connection to come in from the root node, then send out the address of the port they allocate to do further communication, wait for the list of neighbors and for the specialization function, then simply perform it until termination.
To summarize, in the implementation the possibility of sending closures allowed us to obtain a kind of higher order distributed parameterization that kept the runtime code to a minimum size (the source codes of the full system is less than twenty kilobytes).
As far as the general mechanism of closure passing is concerned, no particular requirement/restrictions have been posed onto the physical communication implementation. Even considering the fact that we need to move data between the different processes making up the parallel implementation of an CamlP3l program, we derived no particular constraint onto the communication layer.
Thus, at the very beginning of the CamlP3l project, we faced the problem of choosing a suitable communication system. We had as a goal to come out with the maximum “portability” of CamlP3l. Furthermore, we wanted to fully demonstrate the feasibility of integrating the parallel skeleton world within a functional framework. These two goals had priority over the classical “efficiency and performance” goal one usually has to achieve when dealing with parallelism.
The result is that we have adopted the plain Unix socket world as the communication layer. This has some (very) positive consequences on the overall CamlP3l design:
On the down side, the adoption of Unix sockets presents an evident disadvantage which is the low performance achieved in communications (a raw synchronization (i.e. zero length data communication) takes several milliseconds to be performed, even in those cases when the data transmission media turns out to be free, i.e. no collisions are detected).
At the moment, we are considering to use in the next version of CamlP3l a communication layer based on an optimized communication library such as MPI [18], as an efficient alternative to the socket communication layer, which will be nevertheless retained for its ease of deployment, that makes it attractive for programming courses.
Porting to MPI will require some modifications in the template code used within CamlP3l, and will not necessarily completely solve the performance problems of the socket communication layer when run on a network of computers, where most MPI libraries are still implemented using sockets, but will allow to target real multiprocessor machines where MPI is efficiently implemented, without touching the user code. Also, we will be able to delegate to the MPI system the administrative tasks involved in copying and launching the programs on the different machines.
As far as the process model is concerned, we felt happy with the Unix one. All we need is a mechanism allowing an instance of the template interpreter (the one specialized by using the closure passing mechanism) to be run onto different workstations belonging to a local area network. The Unix rsh mechanism matches this requirement. Note that, as processes are generated and run on different machines just at the beginning of the CamlP3l program execution, any considerations about performance in rsh-ing is irrelevant.
CamlP3l implements each skeleton appearing in the application code by generating a proper instantiation of the corresponding implementation template. In CamlP3l, a single implementation template is provided for each one of the skeletons supported. The implementation templates provided within the current prototype closely resemble the ones discussed in the informal parallel semantics section (Section 1.3). Actually, only the reduce template is slightly different, in that the tree discussed in Section 1.3.7 is actually implemented by a process network similar to the one discussed for the farm, where partially evaluated data is iteratively passed back from the collector to the emitter process. We are currently studying a more efficient mechanism based on a formal calculus for data distribution and computation over dense arrays [17, 8, 7].
Each template appearing in CamlP3l:
val farmetempl : ('a, 'b) Parp3l.action -> in_channel ->
out_channel list -> unit
The process template definition in the CamlP3l code looks like
the following:
let farmetempl (OutChanSel f) ic ocl =
while true do
try
let theoc = f ocl in
match (Marshal.from_channel ic) with
UserPacket(p,seqn,tl) ->
Marshal.to_channel
theoc
(UserPacket (p,seqn,Farmtag::tl))
[Marshal.Closures];
flush theoc;
| EndStream ->
List.iter
(fun x -> Marshal.to_channel
x
EndStream
[Marshal.Closures];
flush x)
ocl;
List.iter close_out ocl; close_in ic; exit 0
with End_of_file -> List.iter close_out ocl;
close_in ic
done;;
Therefore the whole compilation process transforming an CamlP3l skeleton program into the parallel process network implementing the program can be summarized in the following steps:
By providing modules that implement the three CamlP3l skeleton semantics (the sequential one, the parallel one and the graphical one), we allow the CamlP3l user to perform the following parallel application development process:
Let us spend now some words concerning logical, sequential debugging of CamlP3l applications.
A user developing an CamlP3l application may link the sequential skeleton semantics module to his/her code and debug the application by using the plain sequential debugging tools of ocaml. This debugging activity can be performed on a single machine, provided the machine supplies ocaml. Also, performance tuning can be directed using standard sequential profiling tools such as gprof.
Once the application has been debugged, i.e. the user perceives it computes the expected results, he/she can compile the parallel version of the application by linking the parallel skeleton semantics. As we guarantee that the implementation templates for the different skeletons of CamlP3l are correct (deadlock free, load-balanced, etc.) and as we guarantee that the process transforming the skeleton code in the process code is correct, the user does not need to perform explicit activities in order to check that the results computed by the parallel code are correct.
In particular, the user does not need to check that all the processes have been correctly scheduled for execution, or that the communication channels have been set up properly between these processes, or that data of type ’a has been never delivered on channels transmitting data of type ’b. This is a very short list of bad things that may affect the correct behavior of an explicitly parallel program, indeed. The fact that the user is not required at all to take them into account is one of the biggest pro’s of the functional skeleton approach.
Many researchers are currently working on skeletons and most of them are building some kind of parallel implementation, but our work, as far as we know, is unique in its combination of a fully functional strongly typed language with the skeleton approach.
In particular, Darlington’s group at Imperial College in London is actively working on skeletons. They have explored the problems relative to implementing a skeleton programming system, but the approach taken uses an imperative language as the implementation language. Currently there is a “local” prototype implementation but no public domain implementation of their skeleton approach and they seem deeply involved in the study of the data-parallel and coordination aspects of skeletons. [13, 12, 1]
A different approach relative to skeleton parallel programming within a functional framework has been discussed by Bratvold [4]. Bratvold takes into account plain ML programs and looks for skeletons within them, compiling these skeletons by using process networks that look like implementation templates. However, both the final target language and the implementation language are imperative.
Finally, Sérot [23, 22], presents an embedding of skeletons within ocaml that seems to be close to our work, although independently developed. The message passing is performed by interfacing the MPI library with ocaml. The skeletons taken into account are different. She considers data-parallel farm, roughly corresponding to our mapvector skeleton, and two further skeletons, scm and filt. filt is a plain filter skeleton, canceling data items from a list, while scm (Split, Compute and Merge) looks like a map skeleton working on lists with explicit, user defined, decomposition/recomposition functions.
Sérot’s implementation of the skeletons within ocaml is quite different from ours and only allows one skeleton at a time to be realized on the processor networks, thus preventing skeleton composition (you cannot nest two scm skeletons for example), and only allowing for a limited form of staging of the parallel computation: you can perform an scm, then when this is finished, you can reorganize your network and perform another scm. This way, the mapping of virtual processors to real processors on the network is a trivial task, and is done inside each skeleton at run-time instead of beforehand in a specific pass like in CamlP3l. Sérot implements the skeletons included in his model by providing second order functions that directly call MPI and realize an SPMD execution model.
As for the relevant effort done in the field of languages for mobile agents, like for example [16, 15], it should be noted that they address quite a different kind of problems, but once stable, these languages could form the basis of a next generation fully fault-tolerant and dynamically load-balanced version of our system.
Here we showed how a skeleton parallel programming modelcan be successfully married with the functional programming environments such as the one provided by OCaml.
In particular, we discussed a powerful skeletal model, how skeletons can be embedded within OCaml as second order functions and how modules implementing both the sequential and the parallel skeleton and discuss the typical application development cycle in CamlP3l. The whole process preserves the strong typing properties of ocaml.
At the moment, the prototype CamlP3l implementation is being tested as described in this paper and is available from the CamlP3l project home Web page
http://camlp3l.inria.fr/.
In the near future we want first of all to include a more powerful MAP skeleton working on dense arrays with an arbitrary number of dimensions[17, 8, 7]. This will call for a more efficient communication layer, by using colective MPI communications [18] instead of the plainUnix socket library. At the same time, we investigate the feasibility of porting the system on the ubiquitous Windows boxes, for didactical purposes. Finally, we already developed a parallel numerical code [5] and plan to write some more significant parallel applications in order to fully test the prototype.
This document was translated from LATEX by HEVEA.